颜色是通过眼、脑和我们的生活经验所产生的一种对光的视觉效应，我们肉眼所见到的光线，是由频率范围很窄的电磁波产生的，不同频率的电磁波表现为不同的颜色，对色彩的辨认是肉眼受到电磁波辐射能刺激后所引起的一种视觉神经的感觉。
但色彩在电脑里面是如何表示的呢？围绕色彩又有哪些常用的算法呢？请看下文：

颜色表示方法

LMS色彩

人类眼睛有对于长(L, 560-580nm)、中(M, 530-540nm)、短(S, 420-440nm)波长的光感受器(视锥细胞)，因此根据三种视锥细胞的刺激比例，便能描述任一种颜色的感觉，此称为LMS空间
需要注意的是，人类还有一种单色的夜视光感测器(视杆细胞)，其最敏感的感知频谱范围约在490-495nm，约在绿色范围内

CIE色彩

CIE(International Commission on Illumination, 法文Commission internationale de l'éclairage)
基于生理、物理实验等的颜色模型，理论上包括了所有人眼可见光，包括有CIE-RGB、CIE-LAB、CIE-XYZ、CIE-xyY等多种模型，更偏向于色彩理论研究一些。
大写的Y通常都表示感观亮度

YUV/YCrCb色彩

YUV主要用于模拟电视信号，YCrCb主要用于数字视频信号。但大致含义基本是相同的，Y表示明度信息，UVCrCb都是用于描述色度信息，mpeg、jpeg仍然在使用这种色彩表示方式。

当初这么设计的原因有两点：

  1. 人眼对亮度变化更加敏感一些，每一个亮度信息Y都应该单独保存；而人眼对色度变化不那么敏感，相邻的2个或4个像素点可以共用色度信息，可以减少数据大小。
  2. 可以方便兼容黑白电视，只需要取出Y信号就可以了。

换算规则：

$$ \begin{aligned} Y &=& 0.299R + 0.587G + 0.114B \\ U &=& -0.147R - 0.289G + 0.436B \\ V &=& 0.615R - 0.515G - 0.100B \end{aligned} $$

RGB色彩(Red、Green、Blue)

一个物体如果自身发光的话，它发出什么颜色我们就看到什么颜色。
如果是多个色光同时发光，我们看到的是所有色光叠加后的颜色。

颜色加法

使用加法三原色的组合来表示一个点的具体色彩
其中每一个三原色通道的取值范围是[0, 255]
理论上可以表示$255\times255\times255=2^{8+8+8}=16777216$种颜色

LinearRGB

理论上完全按照物理规律的RGB表示法，通常使用[0, 1]范围内的值来表示

sRGB

image

由于人眼特性，人对暗色变化更加敏感，因此肉眼感觉的50度灰实际线性值只有0.214左右。
为了使计算机表示色彩递进关系和人眼感受到的基本一致，微软联合爱普生、HP等制定了sRGB，它的通道值127就对应人眼感受到的中灰（传说中的伽玛校正）。
++通常情况下如果没有特殊说明，一般所说的“RGB”均指sRGB++

AdobeRGB

比sRGB全，包含了所有CMYK色彩

CMYK色彩(Cyan、Magenta、Yellow、Black)

一个物体如果自身不发光的话，我们看到的颜色是它吸收后剩余的颜色。
显然它的三原色就是发光三原色的互补色（为什么防蓝光眼镜看起来偏黄）

颜色减法
颜色减法

使用减法三原色的组合来表示一人点的具体色彩
通常CMYK每一个色彩通道的取值范围是[0, 100]
理论上可以表示$100\times100\times100=1000000$种颜色
换算规则：

$$ \left\{ \begin{aligned} C^{'} &=& \frac{255-R}{255} \\ M^{'} &=& \frac{255-G}{255} \\ Y^{'} &=& \frac{255-B}{255} \end{aligned} \right. $$

$$ K = \min(C^{'}, M^{'}, Y^{'}) $$

$$ \left\{ \begin{aligned} C &=& C^{'} - K \\ M &=& M^{'} - K \\ Y &=& Y^{'} - K \end{aligned} \right. $$

HS?色彩

image

色相(Hue)
: 决定是什么颜色色系，一般情况下H取值范围是[0, 360)

$$ \left\{ \begin{aligned} R{'} &=& R \times \frac{1}{255} \\ G{'} &=& G \times \frac{1}{255} \\ B{'} &=& B \times \frac{1}{255} \end{aligned} \right. $$

$$ \left\{ \begin{aligned} C_{max} &=& \max(R{'}, G{'}, B{'}) \\ C_{min} &=& \min(R{'}, G{'}, B{'}) \\ \Delta C &=& C_{max} - C_{min} \end{aligned} \right. $$

$$ H = \begin{cases} 0^\circ && \Delta C = 0 \\ 60^\circ \times \frac{G{'} - B{'}}{\Delta C} + 0^\circ && C_{max} = R{'} \\ 60^\circ \times \frac{B{'} - R{'}}{\Delta C} + 120^\circ && C_{max} = G{'} \\ 60^\circ \times \frac{R{'} - G{'}}{\Delta C} + 240^\circ && C_{max} = B{'} \\ \end{cases} $$

HSL/HSI色彩(Hue、Saturation、Light/Intensity)

image

饱和度(Saturation)
: 决定颜色的浓淡，取值范围一般[0, 100]

明度(Light)
: 决定颜色有多明亮，取值范围一般[0, 100]

理论上能表示$360\times100\times100=360000$种颜色，但实际会少很多。换算规则：

$$ S = \begin{cases} 0 && \Delta C = 0 \\ 100 \times \frac{\Delta C}{1 - \vert 2L-1 \vert} && \Delta C \ne 0 \end{cases} $$

$$ L = 100 \times \frac{C_{max} + C_{min}}{2} $$

举例：

  1. 纯绿(#00FF00)：H=120, S=100, L=50
  2. 浅绿(#80FF80)：H=120, S=50, L=50
  3. 深绿(#008000)：H=120, S=100, L=25
  4. 纯黑(#000000)：H=~, S=0, L=0
  5. 纯白(#FFFFFF)：H=~, S=~, L=100

HSV/HSB色彩(Hue、Saturation、Value/Brightness)

色轮
锥图

饱和度(Saturation)
: 混入白色的程度，取值范围一般[0, 100]

明度(Brightness)
: 混入黑色的程度，取值范围一般[0, 100]

理论上能表示$360\times100\times100=360000$种颜色，但实际会少很多。换算规则：

$$ S = \begin{cases} 0 && C_{max} = 0 \\ 100 \times (1 - \frac{C_{min}}{C_{max}}) && C_{max} \ne 0 \end{cases} $$

$$ V = 100 \times C_{max} $$

举例：

  1. 纯绿(#00FF00)：H=120, S=100, V=100
  2. 浅绿(#80FF80)：H=120, S=50, V=100
  3. 深绿(#008000)：H=120, S=100, V=50
  4. 纯黑(#000000)：H=~, S=~, V=0
  5. 纯白(#FFFFFF)：H=~, S=0, V=100

常用基本算法

透明叠加算法

假设前景色透明度为$\alpha_{f}$，背景色透明度为$\alpha_{b}$，则计算方式如下：

  1. 最终总透明度与层叠顺序无关。参见方法ColorUtils#compositeAlpha
  2. RGB三个通道计算方式完全相同。参见方法ColorUtils#compositeComponent

$$ \alpha = 1 - (1 - \alpha_{f}) (1 - \alpha_{b}) $$

$$ C = \frac{ \alpha_{f} C{_f} + (1 - \alpha_{f})\alpha_{b} C_{b} } {\alpha} $$

颜色渐变算法

特殊范围渐变

  1. 若渐变起始值和结束值的RGB三个通道有两个完全相等，则对别一通道做线性处理即可(注意需要伽玛校正)

    $$ \left\{ \begin{aligned} C_{ls} = C_{ss}^{2.2} \\ C_{le} = C_{se}^{2.2} \end{aligned} \right. $$

$$ C_{m} = C_{ls} + ratio \times (C_{le} - C_{ls}) $$

$$ C^{'} = \sqrt[2.2]{C_{m}} $$

  1. 若渐变起始值和结束值的HSV三个通道有两个完全相等，则对别一通道做线性处理即可(注意无需伽玛校正)

通用渐变处理

将渐变起始值和结束值的RGB三个通道分别按照特殊范围渐变方法1处理即可(若有透明通道变化则完全按照线性处理，无需伽玛校正)。参见安卓ArgbEvaluator类

对比度亮度算法

  1. 图片的亮度是指将所有像素点取平均值后的数值大小。但因为有RGB三个颜色通道，一般会按照三个通道分别计算后再转成具有亮度值的颜色表示方法。另外由于HSL或HSV的亮度或明度值是完全按照机器值计算的，和人眼主观感受并不相同，所以通常图片的最终亮度是换算成YUV或XYZ表示法后的Y值。\
    如果要增加图片的亮度，只需按照一定规则使像素点平均值增加即可
  2. 图片的对比度是指最亮的点和最暗的点的的比值。为了防止偶尔一个极亮或极暗像素点的偶发影响，一般会取最亮的5%和最暗的5%来参与计算。\
    如果要增加图片的对比度，只需要按照一定规则使各像素点与平均值差值变大即可

假设一幅图片有N个像素点，$p$为调整后的对比度(小于1减小对比度，大于1增加对比度)，$l$为调整后的亮度(小于1减小亮度，大于1增加亮度)，则调整图片的对比度和亮度的算法如下(RGB三个通道计算方式完全相同，只取一个通道说明)：

$$ \overline{C} = \frac{1}{n} \sum_{n=1}^{N}C_n $$

$$ C_n^{'} = p \times (C_n - \overline{C}) + l \times \overline{C} $$

主色提取算法

  1. 将原始图片进行缩放(安卓中默认是$112\times112$)
  2. 缩减图片总颜色数量(RGB888转换成RGB555)
  3. 将所有颜色作为一个统计块放到一个有序队列中(队列顺序按照RGB三个通道各自差值的乘积降序排列)
  4. 从有序队列中取出并移除第一个位置的统计块
  5. 获取取出的统计块RGB三个通道中的差值最大的项
  6. 按照RGB最大差值通道对颜色进行重新排序
  7. 按照颜色统计数量找到位于一半的分割点
  8. 将取出的统计块按照分割点拆分两个统计块
  9. 将新生成的两个统计块加到队列中
  10. 重复步骤4～9，直到队列元素数量不小于最小分类数量(默认16)
  11. 计算每一个统计块的加权平均颜色值

  12. 过滤掉平均值结果中一些特定的颜色

    1. 特别暗的(即HSL的L小于5，接近黑色)
    2. 特别亮的(即HSL的L大于95，接近白色)
    3. 一个红色区间($10\le H \le 37, S\le82$)???

  13. 计算对应文本颜色

    1. 将临时色彩设为纯白，透明度初始设为全不透明
    2. 不段增加临时色彩透明度在一定次数限制内迭代
    3. 将带有透明度的纯白色与统计块的平均色进行合成
    4. 直到合成色与统计块平均色对比度恰好接近某一对比度
    5. 将此时的合成色当作匹配的的文本颜色
    6. 若未找到合适的，则将临时色设成黑色重复1～5步
    7. 优先使标题色和文本色色调一致(即初始临时色相同)

  14. 根据过滤条件获取目标统计结果

    1. 如getDominantSwatch是获取数量最多的颜色
    2. 如getVibrantSwatch饱和度在35以上，亮度在30～70之间的颜色
    3. 如getDarkVibrantSwatch饱和度在35以上，亮度在45以下的颜色
    4. 如getDarkVibrantSwatch饱和度在35以上，亮度在55以上的颜色

颜色变换算法

通过对原图片每一个像素的$RGBA$进行数学变换后，能够得到新颜色$R{'}G{'}B{'}A{'}$，可以得到一些特殊的效果(相机滤镜)

$$ \begin{bmatrix} R^{'} \\ G^{'} \\ B^{'} \\ A^{'} \end{bmatrix} = \begin{bmatrix} R \\ G \\ B \\ A \end{bmatrix} \bigodot \begin{bmatrix} a & b & c & d \\ e & f & g & h \\ i & j & k & l \\ m & n & o & p \end{bmatrix} + \begin{bmatrix} q \\ r \\ s \\ t \end{bmatrix} $$

$$ \left\{ \begin{aligned} R^{'} &=& aR + bG + cB + dA + q \\ G^{'} &=& eR + fG + gB + hA + r \\ B^{'} &=& iR + jG + kB + lA + s \\ A^{'} &=& mR + nG + oB + pA + t \end{aligned} \right. $$

常用矩阵：

  1. 原样矩阵

    $$ \begin{bmatrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{bmatrix} $$

  2. 黑白矩阵

    $$ \begin{bmatrix} 0.299 & 0.587 & 0.114 & 0 & 0 \\ 0.299 & 0.587 & 0.114 & 0 & 0 \\ 0.299 & 0.587 & 0.114 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{bmatrix} $$

  3. 负片(底片)矩阵

    $$ \begin{bmatrix} -1 & 0 & 0 & 0 & 255 \\ 0 & -1 & 0 & 0 & 255 \\ 0 & 0 & -1 & 0 & 255 \\ 0 & 0 & 0 & 1 & 0 \end{bmatrix} $$

常用模糊算法

什么是模糊？当相邻的多个像素点色彩互相影响，使原本清晰可辨的边界无法辨别时就是模糊。

  1. 为了使图片模糊，需要指定一个像素点需要与周围多少个像素点进行相关运算，这个值叫做模糊半径。
  2. 当模糊半径为1时，即相当于需要像素点和它周围8个点按照一定权值比例进行运算

简单算法如下(RGB三个通道计算方式完全相同，只取一个通道说明)：

$$ \begin{matrix} \boxed{C_{tl}} \boxed{C_{tc}} \boxed{C_{tr}} \\ \boxed{C_{ml}} \boxed{C} \boxed{C_{mr}} \\ \boxed{C_{bl}} \boxed{C_{bc}} \boxed{C_{br}} \end{matrix} $$

$$ \begin{bmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \\ \end{bmatrix} $$

$$ C^{'} = \frac{1}{24}C_{tl} + \frac{2}{24}C_{tc} + \frac{1}{24}C_{tr} + \frac{2}{24}C_{ml} + \frac{4}{24}C + \frac{2}{24}C_{mr} + \frac{1}{24}C_{bl} + \frac{2}{24}C_{bc} + \frac{1}{24}C_{br} $$

很显然，模糊矩阵的取值很重要，直接会影响到模糊的效果，是否符合生活中直观感受完全取觉得于它。正太分布就十分符合这种场景，但一般正太分布是一维的，我们需要一个二维正太分布。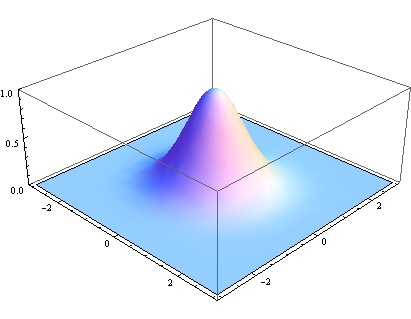
image
正态分布的密码函数叫作“高斯函数”，因此这种模糊算法叫做高斯模糊

简易图片哈希算法

  1. 将图片缩小到$8 \times 8$大小
  2. 将缩小后的图转成灰度图
  3. 计算灰度图片的平均值
  4. 统计像素点，小于平均值记为0，否则记为1
  5. 将64位二进制数据转成8位十六进制值，即为图片哈希
  6. 计算两个哈希间的汉明距离即为相似度

标签: none

添加新评论